凯时

         1、概述
        凯时混合指数是建立在运动粉体液态化混合模型基础上，研究发展而来。
        运动粉体液态化混合模型是描述各种粉体在动态混合中它们的运动趋势。“上浮”、“下沉”分离化运动的趋势越强均匀混合就越困难。
        凯时混合指数就是用数学方法量化描述了这种运动趋势的强弱，成为指导混合工作的依据。因此掌握凯时混合指数的计算和使用方法，就能轻松掌控粉体混合的顺利进行。
        2、粉体特性值的设定
       设每种粉体都可以用其比重乘以其平均粒径做为其特性值。
       表示为：B×D
       其中：   B=粉体的比重  
                     D=粉体的平均粒径
        3、待混粉体特性平均值的设定
       设该批待混合粉体的特性平均值为H，另设Ki为第i种粉体在该批待混合粉体中的占比（百分比），其中占比越大的粉体，对该批待混合粉体的特性平均值影响越大。
       根据上述指导思想特性平均值可用以下方程式表示：               
        H = B1×D1×K1+…+Bi×Di×Ki+…+Bn×Dn×Kn
        归纳为：
 
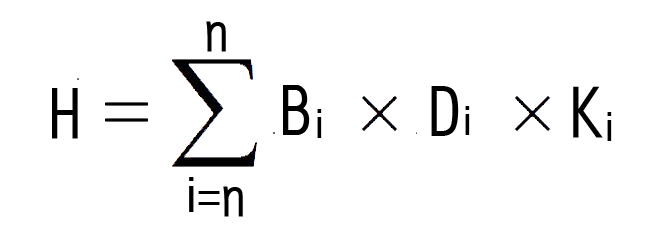
        其中：Bi=第i种粉体的比重 ；
              Di=第i种粉体的粒径 ；
              Ki=第i种粉体所占的百分比 。
              i=1~n
       也就是说这批待混合粉体的特性平均值等于将每一种粉体的比重乘以该粉体的平均粒径再乘以它在该批待混合粉体中的占比的积加在一起求和。
       4、凯时混合指数的定义
       定义：指定粉体的凯时混合指数就是该粉体的特性值与该批待混合粉体特性平均值之比。
        因此有以下公式表示：
 
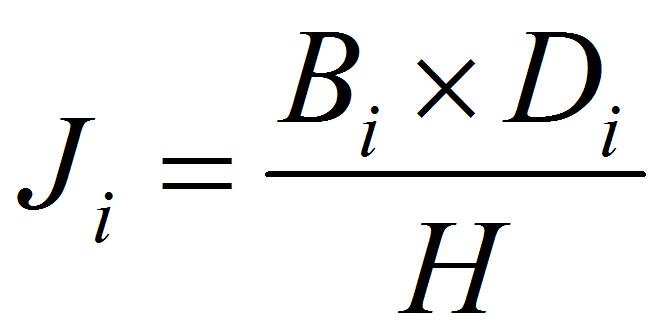
       其中：H = B1×D1×K1+…+Bi×Di×Ki+…+Bn×Dn×Kn                     
       公式中： B1、D1、K1 表示第1种粉体的比重、平均粒径、百分比；
                        Bi、Di、Ki 表示第i种粉体的比重、平均粒径、百分比；
                       n 表示参与混合的粉体种数；
                       H 表示该批待混合粉体的特性平均值；
                      Ji 表示第i种粉体的凯时混合指数；
         当i=1~n时就可以分别计算每种粉体的凯时混合指数J1~Jn。   
         5、举例计算凯时混合指数
        例如现有三种待混合粉体，第一步测出每种粉体可量化的物理指标：比重、平均粒径和在该批待混合粉体中的占比如下：  
       第一种粉体  B1=1.1   D1=0.01mm    K1=30%
       第二种粉体 B2=0.9  D2=0.015mm  K2=60%
       第三种粉体B3=2.1   D3=0.03mm    K3=10%
       第二步计算出特性平均值：
          H =1.1×0.01×30%+0.9×0.015×60%+2.1×0.03×10%
              =0.0033+0.0081+0.0063
              =0.0177
       第三步再计算出三种粉体的凯时混合指数：
            J1=1.1×0.01÷0.0177≈0.62
            J2=0.9×0.015÷0.0177≈0.76
            J3=2.1×0.03÷0.0177≈3.56

二、解读与应用

       1、凯时混合的解读
         1）对指定的一批待混合粉体中每种粉体都有相应的凯时混合指数
          当待混合粉体确定下来之后，就可以通过上述的公式计算出每个粉体相应的凯时混合指数。凯时混合指数越大说明粉体的颗粒大或比重大，凯时混合指数越小说明粉体的颗粒小或比重轻。
          2）一种粉体的凯时混合指数值与自身特性有关还与其他一起待混合的粉体特性有关
         若改变某个粉体的指标会影响其余每一个粉体的凯时混合指数，减少或增加粉体也会改变其余每一个粉体的凯时混合指数。
       2、凯时混合指数的实用意义
        1）凯时混合指数值大小的意义
           ①凯时混合指数值等于1，说明该粉体的比重、平均粒径与整体待混合粉体的均值基本一致，表示该粉体容易参与混合；    
           ②凯时指数值小于1，说明该粉体与整体待混合粉体均值相比，比较轻或比较细，如果其值在0.3以下时，参与混合就比较难以混合均匀了。
          ③凯时指数值大于1，说明该粉体与整体待混合粉体均值相比，比较重或粒径比较大，其值如果在3.0以上时，参与混合就比较难以混合均匀了。通常凯时可以用细化该粉体的平均粒径的方法，减少其凯时混合指数值，从而使混合均匀变的容易。
       2）用凯时混合指数的大小比值定量分析混合工艺的难易程度
         在待混合各种粉体中利用前述公式计算出每一种粉体的凯时混合指数。
         ①选出其中最大凯时混合指数和最小凯时混合指数，并计算出其比值Z：
 
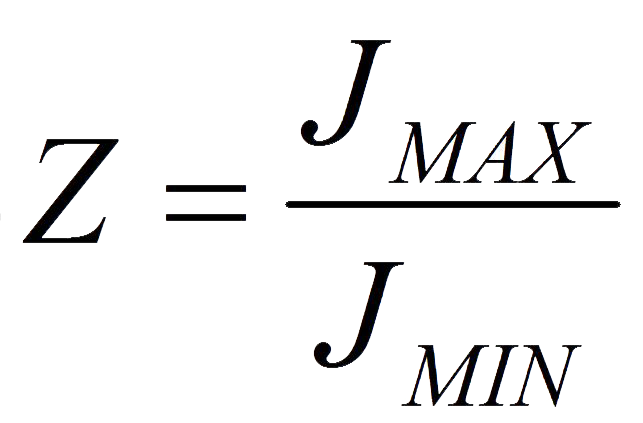
         其中JMAX 为整批粉体中最大的凯时混合指数值，JMIN 为最小的凯时混合指数值。
       ②. 用差异化比值z来判断混合工艺的难易程度：
       通过大量的实验得出以下结论：比值z大于3，说明两种粉体的特性值差别较大，混合均匀的难度开始增加；如果比值z大于6，说明两种粉体的特性值差别特别大，混合均匀是一件不易实现的困难工作。
       3）凯时混合指数的意义
        凯时混合指数之间的差异大小是指数应用的关键，差异越小说明各粉体之间的物理指标接近，属于同质化混合，粉体混合容易达到均匀目标。反之，凯时混合指数差异越大说明存在着粉体差异化混合，粉体之间出现了轻、   重粉等混合工艺难题，混合困难。因此，凯时可以用凯时混合指数来指导粉体混合工艺的顺利进行。
        凯时混合指数是凯时公司设计师团队通过多年的粉体混合经验，科学总结和自主研究推出的理论。
       凯时混合指数的引入就是要对混合工艺的难易程度进行量化描述，这对粉体混合工作提供了很有效的、易于掌握的科学指导方法，填补了国内外工业界粉体混合工艺理论上的一项空白。
        3、凯时混合指数的应用
        凯时混合指数指导混合工作具有很好的实际意义。
       当凯时混合指数的差异化比值z在3以内说明混合任务就易于完成，可采用普通混合设备实施混合。
        当凯时混合指数差异化比值z大于3甚至达到10以上时则混合难度逐步加强甚至难以达到混合均匀的目的。针对这种情况可采用以下方法：
       1）将粉体中较大、较重的颗粒磨细从而降低了指数的差异化比值z，达到了易于混合均匀的目的。
       2）采用有强制混合功能的混合机来解决问题，如双运动®混合机。双运动®混合机的料桶翻滚和裹挟能力能抑制粉体的“上浮”和“下沉”趋势，从而达到了强制混合均匀的目的。    
       4、应用举例
        1）处理前计算出：  
        还以前述的三种粉末为例，并已经计算出相应的凯时混合指数：  
        第一种粉末  B1=1.1   D1=0.01mm      J1≈0.62
        第二种粉末  B2=0.9  D2=0.015mm     J2≈0.76
        第三种粉末  B3=2.1   D3=0.03mm      J3≈3.56
       特性平均值：     H =0.0177
       选出凯时混合指数的最大值和最小值，算出它们的凯时混合指数的大小比值：                                  
       有：   J_MAX=J₃ ≈3.56   J_MIN=J₁≈0.62
        所以比值为： Z=J₃/J₁≈5.74                                                 
       2） 分析：因为第三种粉末与第一种粉末的凯时混合指数差别过大，比值超过了5以上，混合困难。分析其中原因可知，第三种粉末与整体待混合粉末的特性均值差别比较大，是混合困难的主要原因。建议对第三种粉末细化处理。因为第一种、第二种粉末的凯时混合指数比较接近，而第三种粉末的凯时混合指数比它们大出许多，同时第一种、第二种粉末属于小粉、轻粉不能粗化，所以凯时只有通过磨细第三种粉末，使其凯时混合指数相互接近，从而达到方便混合均匀的目的！
       3）将第三种粉末磨细后：
       得出第三种粉末的特性值改变：   
         a1        B1=1.1       D1=0.01mm      K1=30%
         b1        B2=0.9       D2=0.015mm     K2=60%
         c1        B3=1.2       D3=0.016mm     K3=10%
      重新计算特性平均值：
        H = 1.1×0.01×30%+0.9×0.015×60%+1.2×0.016×10%
           ≈0.0033+0.0081+0.0019
           ≈0.013
       重新计算每种粉末的凯时混合指数：
        J1=1.1×0.01÷0.013≈0.85
        J2=0.9×0.015÷0.013≈1.04
        J3=1.2×0.016÷0.013≈1.48
       选出最大凯时混合指数和最小凯时指数，算出比值Z：Z=JMAX/JMIN=J3/J1≈1.74
通过处理可以看出三种粉末的凯时混合指数差别已经很小，比值Z小于2，这说明第三种粉末与其他两种粉末特性比较接近了，在这样的条件下，就很容易达到混合均匀的目标。这样就很好地利用了凯时混合指数指导混合工艺的顺利进行！
       5、小结
      总结得出凯时混合指数有三大优点：
       1）量化各种粉体混合任务的难易程度。
       2）在各种参与混合的粉体中精准指出不易混合均匀的个体，方便做出针对性工作指导混合工作的顺利进行。
       3）通过凯时混合指数的简单检测、计算就可指导混合工艺的实施，节省了大量的人力、物力和时间的损耗。